Our main research focus is using computational methods combined with analytical tools to study novel phenomena due to strong correlations in many-body systems. In the past few years, we have studied a wide variety of correlated systems to elucidate the underlying physics within. Furthermore, we are also advancing numerical methods that enable us to study previously unattainable problems.

Tensor Network

TN+QMC

We propose an efficient numerical method, which combines the advantages of recently developed tensor-network based methods and standard trial wave functions, to study the ground-state properties of quantum many-body systems. In particular, this allows us to also represent states that do not obey the area law of entanglement entropy. In addition, for fermionic systems, the fermion sign structure can be encoded in the input wave function.

Variational Monte Carlo simulations using tensor-product projected states, O. Sikora, H.-W. Chang, C.-P. Chou, F. Pollmann, and Y.-J. Kao, Phys. Rev. B. 91, 165113 (2015).

TN+Dissipative Systems

Directly in the thermodynamic limit, we show how to combine imaginary and real time evolution of tensor networks to efficiently and accurately find the nonequilibrium steady states (NESS) of one-dimensional dissipative quantum lattices governed by the Lindblad master equation. The imaginary time evolution first bypasses any highly correlated portions of the real-time evolution trajectory by directly converging to the weakly correlated subspace of the NESS, after which real time evolution completes the convergence to the NESS with high accuracy. We demonstrate the power of the method with the dissipative transverse field quantum Ising chain. We show that a crossover of an order parameter shown to be smooth in previous finite-size studies remains smooth in the thermodynamic limit.

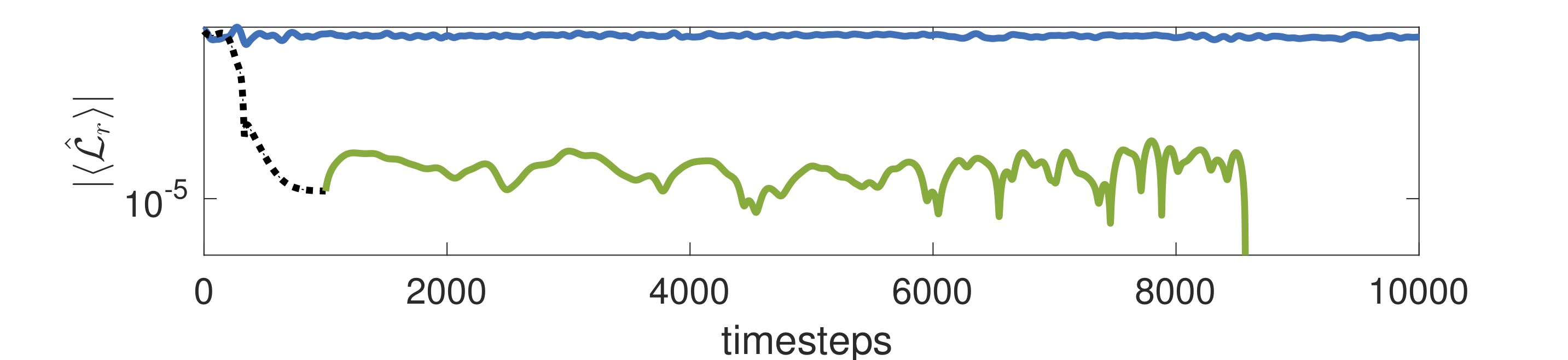
Steady States of Infinite-Size Dissipative Quantum Chains via Imaginary Time Evolution, A. A. Gangat, I. Te, and Y.-J. Kao, Phys. Rev. Lett. 119, 010501 (2017).

TN+Frustrated Magnetism

A preponderance of evidence suggests that the ground state of the nearest-neighbor $S=1/2$ antiferromagnetic Heisenberg model on the kagome lattice is a gapless spin liquid. Many candidate materials for the realization of this model possess in addition a Dzyaloshinskii-Moriya (DM) interaction. We study this system by tensor-network methods and deduce that a weak but finite DM interaction is required to destabilize the gapless spin-liquid state. The critical magnitude, $D_c/J≃0.012(2)$, lies well below the DM strength proposed in the kagome material herbertsmithite, indicating a need to reassess the apparent spin-liquid behavior reported in this system.

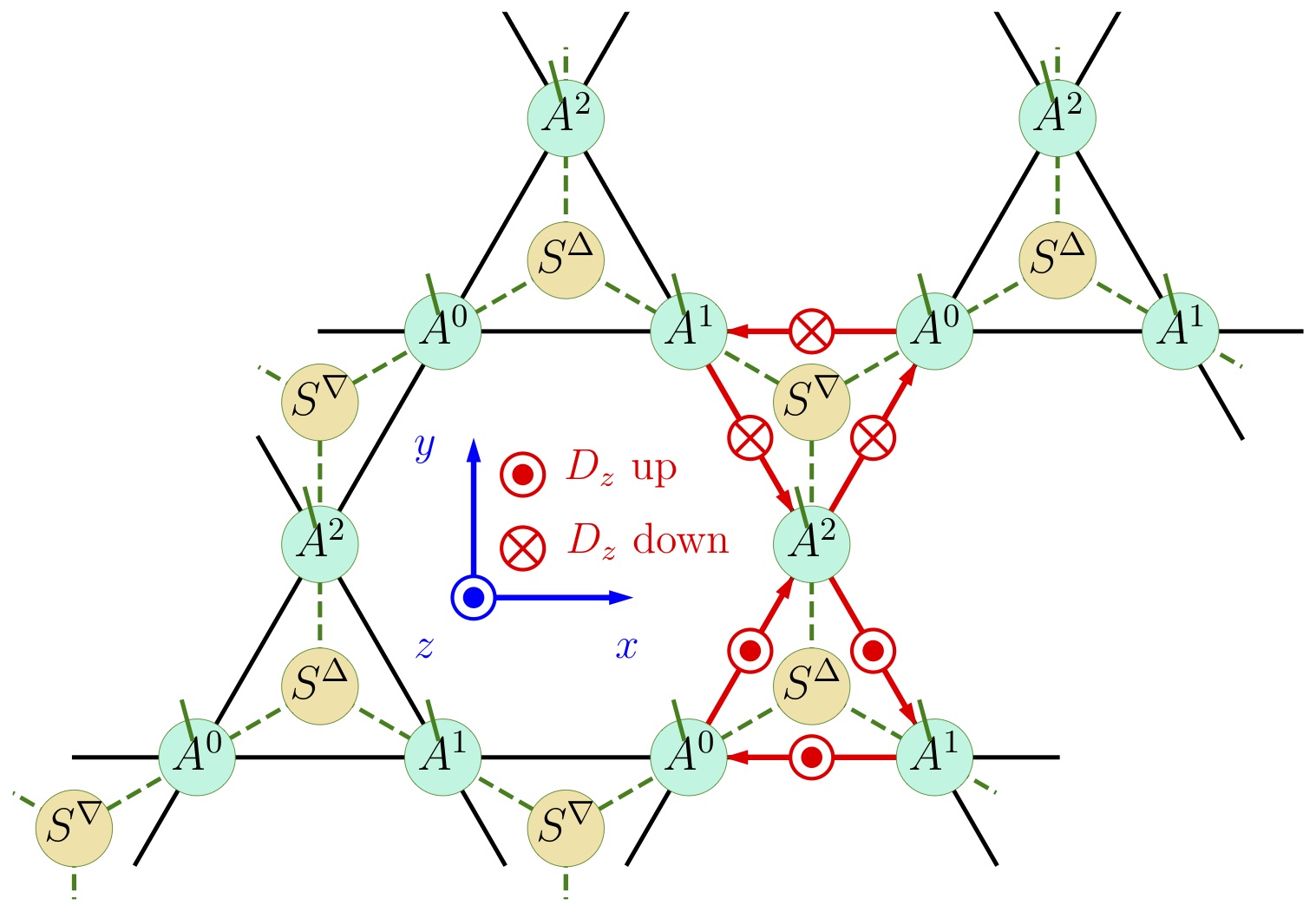
Gapless spin liquid in the kagome Heisenberg antiferromagnet with Dzyaloshinskii-Moriya interactions, Chih-Yuan Lee, B. Normand, Ying-Jer Kao, arXiv:1809.09128, Phys. Rev. B 98, 224414 (2018).

TN+Disordered Systems

Using a strong-disorder renormalization group method formulated as a tree tensor network, we study the zero-temperature phase of the quantum Ising chain with bond randomness. Our results demonstrate an infinite-randomness quantum critical point in zero longitudinal field accompanied by pronounced quantum Griffiths singularities, arising from rare ordered regions with anomalously slow fluctuations inside the paramagnetic phase. Upon application of a longitudinal field, the quantum phase transition between the paramagnetic phase and the antiferromagnetic phase is completely destroyed.

Griffiths singularities in the random quantum Ising antiferromagnet: A tree tensor network renormalization group study, Y.-P. Lin, Y.-J. Kao, P. Chen, and Y.-C. Lin, Phys. Rev. B 96, 064427 (2017).

Universal Tensor Network Library (Uni10)

Uni10 is an open-source C++ library designed for the development of tensor network algorithms. Programming tensor network algorithms is tedious and prone to errors. The task of keeping track of tensor indices while performing contraction of a complicated tensor network can be daunting. It is desirable to have a platform that provides bookkeeping capability and optimization.

This software distinguishes itself from other available software solutions by providing the following advantages:

Fully implemented in C++.
Aimed toward applications in tensor network algorithms.
Provides basic tensor operations with an easy-to-use interface.
Provides a Network class to process and store the details of the graphical representations of the networks.
Provides a collection of Python wrappers which interact with the Uni10 C++ library to take advantage of the Python language for better code readability and faster prototyping, without sacrificing the speed.
Provides behind-the-scene optimization and acceleration.

For more information on Uni10, please check official website http://uni10.org.

Frustrated Magnetism

Classical and Quantum Spin Ice

Using Monte Carlo simulations, we identify a new phase in dipolar spin ice with a half-magnetization plateau. This half-polarized phase should correspond to a quantum solid phase in an effective 2D quantum boson model, and the transition from the Coulomb phase with a power-law correlation to this state can be regarded as a superfluid to a quantum solid transition.

Half-magnetization plateau of a dipolar spin ice in a [100] field, S. -C. Lin and Y. -J. Kao, Phys. Rev. B 88, 220402(2013).

In collaboration with experimentalists, we report report the first experimental evidence of a Higgs transition of the emergent magnetic monopoles from a magnetic Coulomb liquid to a ferromagnet in a material Yb₂Ti₂O₇ known as the quantum spin ice. By cooling Yb₂Ti₂O₇ to 0.21 K, the team observed a transition from a state with fractionalized unstable monopoles to a ferromagnetic state with condensed stable monopoles, indicating a Higgs transition of monopoles. This implies that the ferromagnetic state can be regarded as a superconducting state of the magnetic monopoles, where the dissipationless monopole current can occur.

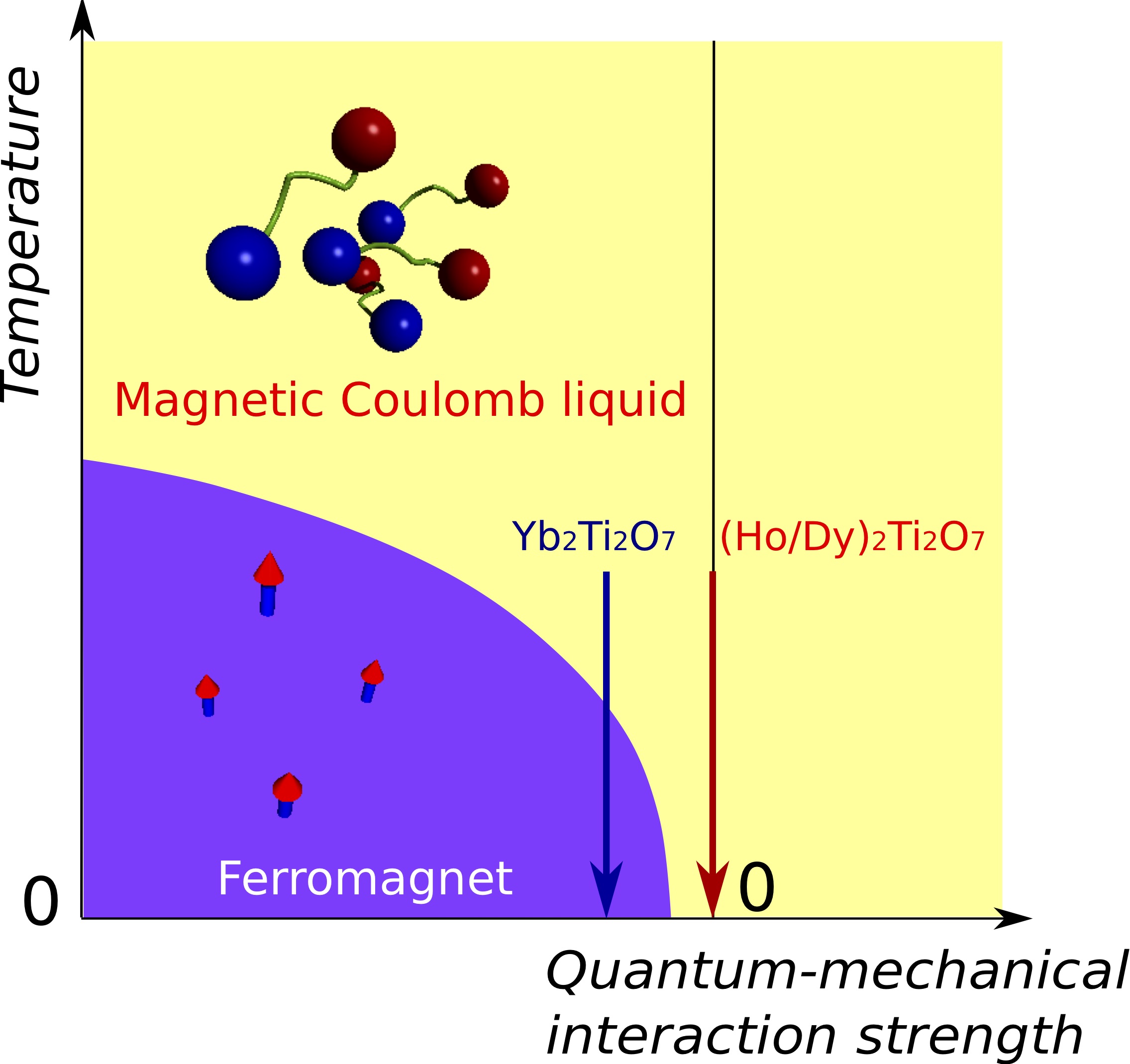
Higgs transition from a magnetic Coulomb liquid to a ferromagnet in Yb₂Ti₂O₇, Lieh-Jeng Chang, Shigeki Onoda, Yixi Su, Ying-Jer Kao, Ku-Ding Tsuei, Yukio Yasui, Kazuhisa Kakurai, Martin Richard Lees, Nat. Comm. 3, 992 (2012).

We study the topological entanglement entropy and the thermal entropy of a quantum ice model on a geometrically frustrated kagome lattice. We find that the system does not show a $Z_2$ topological order down to extremely low temperature, yet continues to behave like a classical kagome ice with finite residual entropy. Our theoretical analysis indicates an intricate competition of off-diagonal and diagonal quantum tunneling processes leading to a suppression of the quantum energy scale.

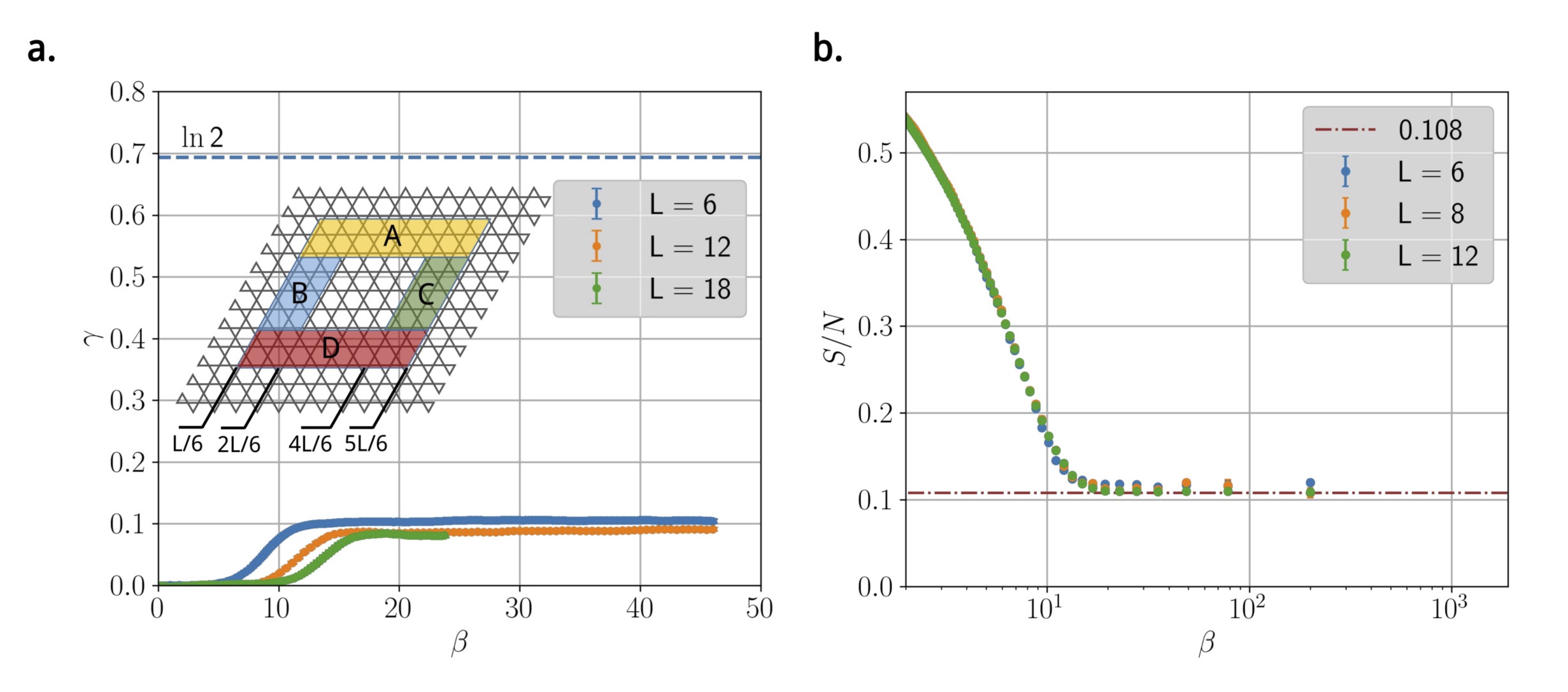
Tunneling-induced restoration of classical degeneracy in quantum kagome ice, Kai-Hsin Wu, Yi-Ping Huang, Ying-Jer Kao, arXiv:1806.08145 Phys. Rev. B 99, 134440 (2019).

Classical and Quantum Phase Tranistions

Finite-size scaling method for the Berezinskii-Kosterlitz-Thouless transition

We test an improved finite-size scaling method for reliably extracting the critical temperature $T_{\rm BKT}$ of a Berezinskii-Kosterlitz-Thouless (BKT) transition. For the Monte Carlo calculations we use GPU (graphical processing unit) computing to obtain high-precision data for $L$ up to 512. We find that the sub-leading logarithmic corrections have significant effects on the extrapolation and we obtain the best estimate of $T_{\rm BKT}$ = 0.8935(1).

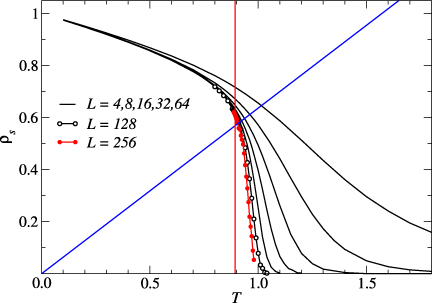
Finite-size scaling method for the Berezinskii–Kosterlitz–Thouless transition, Yun-Da Hsieh, Ying-Jer Kao, Anders W Sandvik, J. Stat. Mech. (2013) P09001.

Quantum phase transitions driven by rhombic-type single-ion anisotropy

We map out the full phase diagram of the $S=1$ spin chain with both the uniaxial-type, $D(S^z)^2$, and the rhombic-type, $E[(S^x)^2-(S^y)^2]$ single-ion anisotropy. The topological critical points are determined by the level spectroscopy method with a newly developed parity technique in the density-matrix renormalization group and the Haldane-Large-$D$ critical point is obtained with an unprecedented precision, $(D/J)_c$ =0.9684713(1).

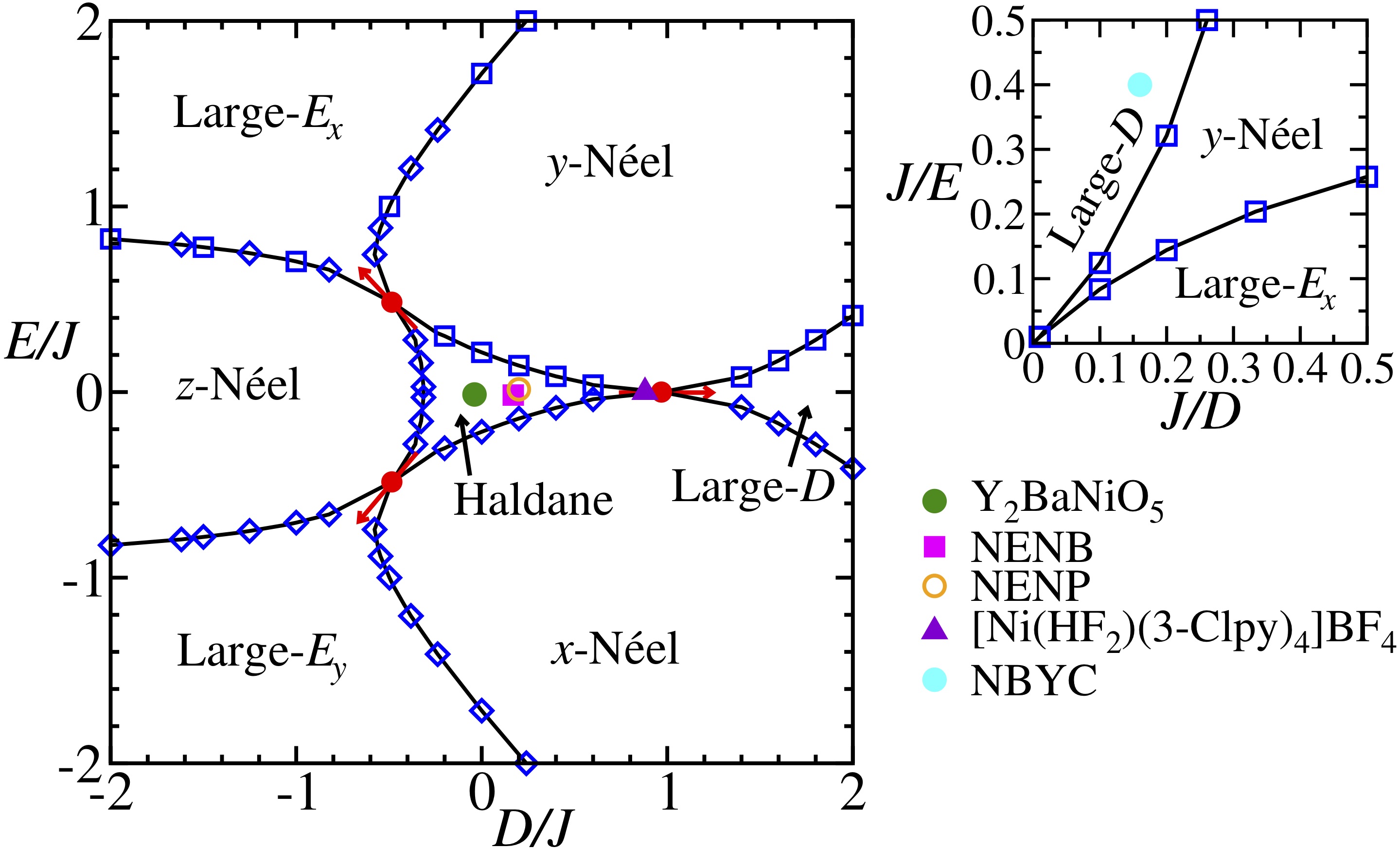
Quantum phase transitions driven by rhombic-type single-ion anisotropy in the S=1 Haldane chain, Y.-C. Tzeng, H. Onishi, T. Okubo, and Y.-J. Kao, Phys. Rev. B 96, 060404 (2017).

Machine Learning

Reinforcement Learning in Topologically Constrained Systems

We develop a deep reinforcement learning framework where a machine agent is trained to search for a policy to generate a ground state for the square ice model by exploring the physical environment. After training, the agent is capable of proposing a sequence of local moves to achieve the goal. Analysis of the trained policy and the state value function indicates that the ice rule and loop-closing condition are learned without prior knowledge.
We test the trained policy as a sampler in the Markov chain Monte Carlo and benchmark against the baseline loop algorithm. This framework can be generalized to other models with topological constraints where generation of constraint-preserving states is difficult.

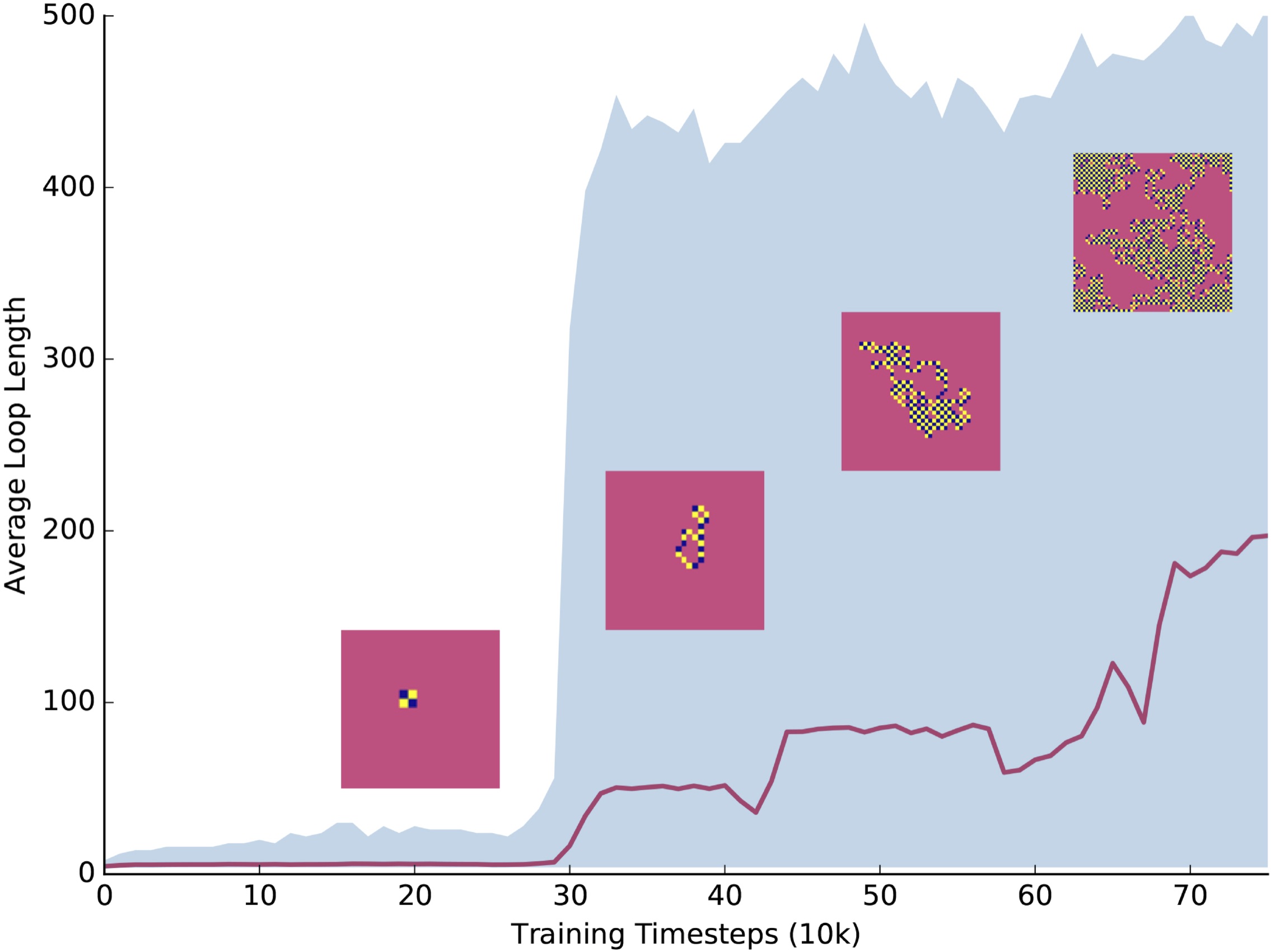
Generation of ice states through deep reinforcement learning, Kai-Wen Zhao, Wen-Han Kao, Kai-Hsin-Wu and Ying-Jer Kao arXiv:1903.04698 Phys. Rev. E 99, 062106 (2019).

Our Research